宇宙中存在由质量相等的四颗星组成的四星系统,四星系统离其他恒星较远,通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动;另一种形式是有三颗星位于等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行,而第四颗星刚好位于三角形的中心不动.已知每个星体的质量均为m,引力常量为G.试求:
(1)第一种形式下,星体运动的线速度.
(2)第一种形式下,星体运动的周期;
(3)假设两种形式星体的运行周期相同,求第二种形式下星体运动的轨道半径.
(1)第一种形式,设轨道半径为r,则据几何关系有:r=
a2 2
以任一星体为研究对象,作受力图有:
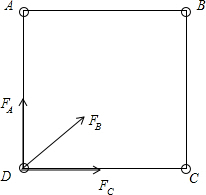
∵如图以D为研究对象,D受三个力的合力提供D围绕圆周运动的向心力则有:
G
+2Gm2 (
a)22
cos450=mm2 a2 v2 r
∴v=(4+
)Gm2 4a
(2)根据周期定义有:
T=2πr v
∴可得:T=2πa2a (4+
)Gm2
(3)第二种形式,设轨道半径为R,则位于等边三角形顶点的两星间距离为:L=2Rcos30°以做圆周运动的任一星体为研究对象:
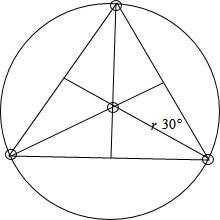
∵G
+2Gm2 R2
cos300=m(m2 L2
)2R2π T
∴R=a3 6+2 3 12+3 2
答:(1)第一种形式下,星体运动的线速度v=
.(4+
)Gm2 4a
(2)第一种形式下,星体运动的周期T=2πa
;2a (4+
)Gm2
(3)假设两种形式星体的运行周期相同,求第二种形式下星体运动的轨道半径R=a
.3 6+2 3 12+3 2
