问题
单项选择题
设f(x)在(-∞,+∞)上有定义,在(-∞,0)∪(0,+∞)内可导,x=0为f(x)的可去间断点,则下列结论正确的是
A.x=0为f'(x)的可去间断点.
B.x=0为f'(x)的跳跃间断点.
C.x=0为
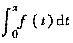 的可去间断点.
的可去间断点.
D.x=0为
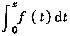 的连续点.
的连续点.
答案
参考答案:D
解析:[分析一] 因f(x)在(-∞0)∪(0,+∞)内可导,从而f(x)分别在(-∞,0)与(0,+∞)上连续,又因x=0是f(x)的可去间断点,从而补充定义[*],补充定义后的函数f(x)就在区间(-∞,+∞)上连续.于是[*]在(-∞,+∞)内可导,特别在x=0处连续.由于改变函数在个别点的函数值不影响函数的可积性与定积分的值(这是定积分的性质之一),所以[*]也在x=0处连续.即应选(D).
[分析二] 用排除法.
对于(A):取[*]则[*]从而可知x=0为f'(x)的跳跃间断点.故(A)不对.
对于(B):取[*]则对任何x≠0都有f'(x)=0,从而可知x=0为f'(x)的可去间断点.故(B)不对.
对于(C):同样取[*]则不仅有[*],而且对任何x≠0都有[*],可见x=0不是[*]的可去间断点.故(C)也不对.
由排除法可知,应选(D).
