问题
单项选择题
设f(x)=(1+x+x2)esinx,则f"(0)=
A.0.
B.2.
C.
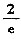 .
.
D.5.
答案
参考答案:D
解析:
[分析]: 令u(x)=1+x+x2,则u(0)=1,u'(0)=1,u"(0)=2;令v(x)=esinx,则v(0)=1,v'(0)=cosx·esinx|x=0=1,v"(0)=(-sinx·esinx+esinx·cos2x)|x=0=1,又
f(x)=u(x)v(x),f'(x)=u'(x)v(x)+u(x)v'(x),
f"(x)=u"(x)v(x)+u'(x)v'(x)+u'(x)v'(x)+u(x)v"(x)
=u"(x)v(x)+2u'(x)v'(x)+u(x)v"(x),
于是 f"(0)=u"(0)v(0)+2u'(0)v'(0)+u(0)v"(0)=2+2+1=5.
故应选(D).
[*]
