问题
单项选择题
设函数f(u)可导,且y+z=xf(y2-x2)确定隐函数z=z(x,y),则
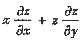 =
=
答案
参考答案:C
解析:
[分析]: 令u=y2-x2,方程y+x=xf(y2-z2)就可以改写成y+z=xf(u).把它看成关于自变量x与y的恒等式,两端求全微分即得
dy+dz=f(u)dx+xf'(u)du
[*]dy+dz=f(y2-z2)dx+f'(y2-z2)(2ydy-2zdz),
整理得
[1+2xzf'(y2-z2)]dz=f(y2-z2)dx+[2xyf'(y2-z2)-1]dy,
从而 [*]
这样一来就有
[*]
故应选(C).
