问题
问答题
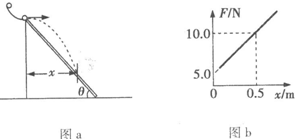
如图a所示研究小球在斜面上做平抛运动的实验装置,每次将质量为m的小球从半径为R的四分之一圆弧形轨道不同位置静止释放,并在弧形轨道最低点水平部分处装有压力传感器测出小球对轨道压力的大小F.已知斜面与水平地面之间的夹角θ=45°,实验获得小球在斜面上的不同水平射程x,最后作出了如图b所示的F-x图象,g=10m/s2,则由图可求得小球的质量m=______,四分之一圆弧形轨道半径R=______.
答案
由图可得,当平抛的距离是0时,即小球的速度是0时,即小球静止时,小球对轨道的压力是5.0N,所以小球的质量:
m=
=G g
=F0 g
=0.5kg5.0 10
设小球水平抛出时的速度为v0,由牛顿运动定律得:
F-mg=m
…①v02 R
由平抛运动规律和几何关系有,小球的水平射程:
x=s=v0t…②
小球的竖直位移:
y=h=
gt2…③1 2
由几何关系有:
y=xtanθ…④
由②③④有:x=
…⑤2v02tanθ g
由①⑤有:F=mg+mg 2Rtanθ
由图象知:
=mg 2Rtanθ 10.0-5.0 0.5
解得:R=0.25m
故答案为:0.5kg,0.25m.
