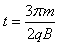问题
计算题
如图所示,无重力空间中有一恒定的匀强磁场,磁感应强度的方向垂直于xOy平面向外,大小为B,沿x轴放置一个垂直于xOy平面的较大的荧光屏,P点位于荧光屏L,在y轴上的A点放置一放射源,可以不断地沿平面内的不同方向以大小不等的速度放射出质量为m、电荷量为+q的同种粒子,这些粒子打到荧光屏上能在屏上形成一条亮线.P点处在亮线上。已知OA=OP=l,求:
(1)若能打到P点,则粒子速度的最小值为多少?
(2)若能打到P点,则粒子在磁场中运动的最长时间为多长?
答案
解:(1)粒子在磁场中运动,洛伦兹力提供向心力,要粒子通过A、P两点,则有A、P关于运动轨迹的直径对称。设粒子的速度大小为v时,其在磁场中的运动半径为R,则F=qBv
由牛顿运动定律有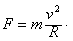
若粒子以最小的速度到达P点时,其轨迹一定是以AP为直径的圆(如图中圆O1所示)
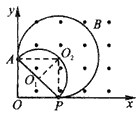
由几何关系知: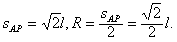
则粒子的最小速度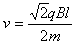
(2)粒子在磁场中的运动周期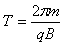
设粒子在磁场中运动时其轨迹所对应的圆心角为θ,则粒子在磁场中的运动时间为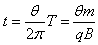
由图可知,在磁场中运动时间最长的粒子的运动轨迹如图中圆O2所示,此时粒子的初速度方向竖直向上
则由几何关系有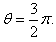
则粒子在磁场中运动的最长时间