问题
计算题
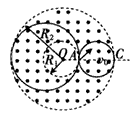
如图甲所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在辐射状电场和垂直纸面的匀强 磁场,内外圆间的电势差U为常量,R1=R0,R2=3R0。一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力。
(1)已知粒子从外圆上以速度v1射出,求粒子在A点的初速度v0的大小。
(2)若撤去电场,如图乙所示,已知粒子从OA延长线与外圆的交点C以速度V2射出,方向与OA延长线成 45°角,求磁感应强度的大小及粒子在磁场中运动的时间。
(3)在图乙中,若粒子从A点进入磁场,速度大小为v3,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少?

答案
解:(1)以粒子为研究对象,由动能定理: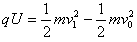
得: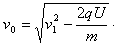
(2)设磁场的磁感应强度为B,带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,设圆的半径为r,有: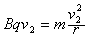
由几何关系得:r2+r2=(R2-R1)2
解得: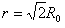
由以上两式可以解得:
根据公式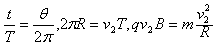
解得:
(3)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,粒子的速度方向沿垂直于AC方向,设半径为r1,要使粒子一定能够从外圆射出,则必满足:2r1>R2+R1
由 ,联立以上各式得:
,联立以上各式得: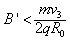
比较以上两种情况,应当是第二种情况磁场最小,即
