问题
计算题
如图所示，在真空中半径r=3.0×10-2 m的圆形区域内，有磁感应强度B=0.2T、方向垂直于纸面向里的匀强磁场。一批带正电的粒子以初速度v0=1.0×106 m/s从磁场边界上的一点a向着纸面内的各个方向射入磁场，该粒子的比荷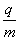
=1.0×108 C/kg，不计粒子重力。
(1)求粒子在磁场中运动的最长时间；
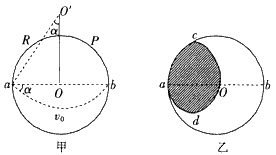
(2)若射入磁场时的速度改为v0=3.0×105 m/s，其他条件不变，试用斜线在图中描绘出该粒子可能出现的区域。
答案
解：粒子在磁场中运动的圆弧所对应的圆心角最大时，粒子在磁场中运动的时间最长，以此求出最长时间。根据粒子由a点向着各个方向射入磁场，画出它们的轨迹示意图，确定粒子在磁场中可能出现的区域
(1)粒子以速度v0=1.0×106 m/s射入磁场，在洛伦兹力作用下做匀速圆周运动，则有：
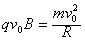
解得：R=5.0×10-2 m
其最长时间tm=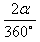
×T
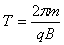
由三角形可知sinα=0.6，得α=37°
解得：tm=6.5×10-8 s
(2)当v0=3.0×105 m/s时，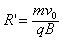
=1.5×10-2 m=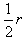
由于粒子逆时针方向做圆周运动，因此粒子能到达的位置边缘是以aO为直径的半圆弧adO和以a为圆心、r为半径的圆弧Oc
即粒子在磁场中可能出现的区域为图乙中画斜线的部分