问题
计算题
一艘客轮因故障需迅速组织乘客撤离。乘客在甲板上须利用固定的绳索下滑到救援快艇上。绳索与竖直方向的夹角θ=37°,设乘客下滑过程绳索始终保持直线。为保证行动又快又安全,乘客先从静止开始匀加速滑到某最大速度,再匀减速滑至快艇,速度刚好为零,加速过程与减速过程中的加速度大小相等。在乘客开始下滑时,船员同时以水平速度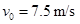 向快艇抛出救生圈刚好落到救援快艇上(快艇可视为质点),如图所示。并知乘客下滑的时间是救生圈平抛下落的2倍,不计空气阻力,重力加速度g取10 m/s2,sin37°= 0.6,cos37°=0.8,求:
向快艇抛出救生圈刚好落到救援快艇上(快艇可视为质点),如图所示。并知乘客下滑的时间是救生圈平抛下落的2倍,不计空气阻力,重力加速度g取10 m/s2,sin37°= 0.6,cos37°=0.8,求:

(1)乘客沿着绳索下滑的时间t;
(2)乘客下滑过程的最大速度vm。
答案
(1)4s(2)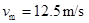
题目分析:(1)设救生圈平抛运动的时间为t0,由平抛运动规律,有
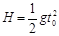 , H tanθ=v0t0 (4分)
, H tanθ=v0t0 (4分)
联立以上各式,得 H=20m, t0=2s (2分)
由题意可知t=2t0=4s (2)
(2)由几何关系,得绳索长L=H/cos37°=25 m (2分)
因加速过程与减速过程的加速度相等,所以甲在绳索中点处速度最大,
由 (2分)
(2分)
代入数据,得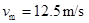 (1分)
(1分)
