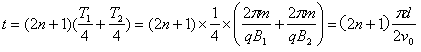问题
计算题
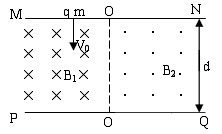
如图所示,在直线MN与PQ之间有两个匀强磁场区域,两磁场的磁感应强度分别为B1、B2,方向均与纸面垂直,两磁场的分界线OO′与MN和PQ都垂直。现有一带正电的粒子质量为m、电荷量为q,以速度V0垂直边界MN射入磁场B1,并最终垂直于边界PQ从O′Q段射出,已知粒子始终在纸面内运动,且每次均垂直OO′越过磁场分界线。
(1)写出MN与PQ间的最小距离d的表达式;
(2)用d、V0表示粒子在磁场中运动的时间。
答案
解:(1)粒子在O'Q间射出,轨迹如图所示
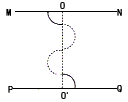
由qv0B=mv02/R,得R1=mv0/qB1
同理得R2=mv0/qB2
又最小距离为d=R1+R2
因此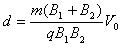
(2)粒子在磁场B1中做圆周运动的周期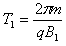
在磁场B2中做圆周运动的周期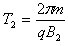
粒子在O'Q间射出,在两个磁场中分别经历(2n十1)个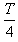
所以