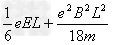问题
计算题
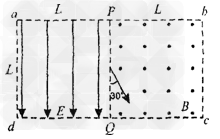
如图所示，虚线框abcd内为边长均为L的正形匀强电场和匀强磁场区域，电场强度的大小为E，方向向下，磁感应强度为B，方向垂直纸面向外，PQ为其分界线，现有一群质量为m，电荷量为-e的电子(重力不计)从PQ中点与PQ成30°角以不同的初速射入磁场，求：
(1)能从PQ边离开磁场的电子在磁场运动的时间．
(2)若要电子在磁场运动时间最长，其初速v应满足的条件？
(3)若电子在满足(2)中的条件下且以最大速度进入磁场，最终从电场aP边界飞出虚线框所具有的动能Ek。
答案
解：(1)由洛仑兹力充当向心力：eBv=m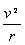
①
电子在磁场中运动的周期：T=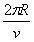
②
①②解得：T=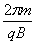
能从PQ边进入电场(如图)．粒子在匀强磁场中运动时间为t，由图知t=
T ③
解得：t=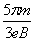
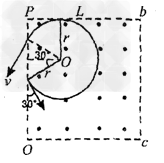
(2)当电子轨迹与Pb边相切时，有满足条件的最大速度v，由几何关系知其轨道半径r满足
r+rsin30°=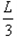
④ r=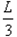
洛仑兹力充当向心力：eBv=m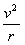
①④解得v=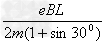
=
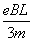
因此，当v≤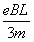
时，电子有磁场运动有最长时间
(结果表示为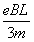v<
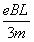，0<v<
，0<v≤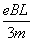
均正确)
(3)以最大速度v进入电场，且从aP边飞出时电子有最大动能EKM，由动能定理：
eE(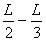
)=Ekm-
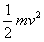⑥
解得Ekm=