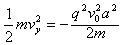问题
计算题
如图所示，左右两个矩形区域中存在着方向相反的匀强磁场，磁感应强度均为B。两磁场区域的宽度为a，长度为(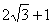
)a，两磁场相距2a。有一质量为m，电荷量为+q的带电粒子(重力不计)，从左侧磁场的P点沿与水平成30°角的方向射入磁场。
(1)若让带电粒子从边界MN穿出，且时间最短，求带电粒子初速度v0和最短时间t；
(2)若在中间区域加一竖直方向的匀强电场，带电粒子以(1)问中的速度v0通过左侧磁场区域后经过电场力的作用，恰好能垂直射入右侧磁场区域。求电场强度E和电场力做的功W。
答案
解：(1)带电粒子在磁场中运动的周期为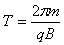
，带电粒子速度越大，经过磁场和非磁场区域的时间越短，但是要保证带电粒子不能从左侧磁场区域的左侧或右侧磁场区域的右侧穿出磁场，所以可根据题意画出如图所示的带电粒子运动的轨迹图。
由图象可析可得，带电粒子在左侧磁场区域运动的圆心角为120°，半径r=2a
根据
，可得
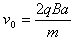
带电粒子在左侧磁场区域运动的时间为t1=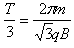
在中间没有磁场的区域，带电粒子做匀速直线运动，所需时间为t2=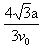
=
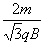
根据几何关系，带电粒子在第一次经过左侧磁场区域时竖直方向的位移为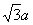
，经过中间无磁场的区域竖直方向的位移为a，竖直方向的位移还剩
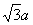，根据对称性，带电粒子经过右侧磁场区域的时间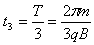
综上所述，带电粒子经历的总时间为t=t1+t2+t3=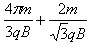
(2)带电粒子穿出左侧磁场的速度与水平方向成30°角
水平方向的速度vx=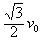
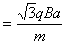
竖直方向的速度vy=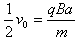
若让带电粒子恰好能垂直射入右侧磁场，带电粒子竖直方向的速度需要变为零
根据2a=vxt，0=vy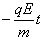
，解得
电场力做的功等于竖直方向动能的变化W=0-