问题
计算题
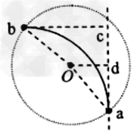
如图，一半径为R的圆表示一柱形区域的横截面（纸面）。在柱形区域内加一方向垂直于纸面的匀强磁场，一质量为m、电荷量为q的粒子沿图中直线在圆上的a点射入柱形区域，在圆上的b点离开该区域，离开时速度方向与直线垂直。圆心O到直线的距离为l。现将磁场换为平等于纸面且垂直于直线的匀强电场，同一粒子以同样速度沿直线在a点射入柱形区域，也在b点离开该区域。若磁感应强度大小为B，不计重力，求电场强度的大小。
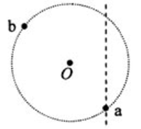
答案
解：粒子在磁场中做圆周运动。设圆周的半径为r，由牛顿第二定律和洛仑兹力公式得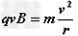
①
式中v为粒子在a点的速度
过b点和O点作直线的垂线，分别与直线交于c和d点。由几何关系知，线段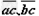
和过a、b两点的轨迹圆弧的两条半径（未画出）围成一正方形。因此
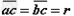②
设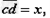
由几何关系得
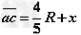③
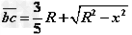④
联立②③④式得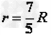
再考虑粒子在电场中的运动。设电场强度的大小为E，粒子在电场中做类平抛运动。设其加速度大小为a，由牛顿第二定律和带电粒子在电场中的受力公式得qE=ma ⑥
粒子在电场方向和直线方向所走的距离均为r，有运动学公式得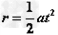
⑦
r=vt ⑧
式中t是粒子在电场中运动的时间。联立①⑤⑥⑦⑧式得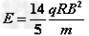
⑨