（Ⅰ）若a=1，则f（x）=（x²-2x+1）e^x，f′（x）=（x ²-1）e^x

∴切线的斜率k=f′（2）=3e²

又切点的坐标为（2，e²），

∴切线方程为y-e²=3e²（x-2），即3e²x-y-5e²=0

（Ⅱ）由f′（x）=[ax²+（a-1）x-a]e^x

得h（x）=f（x）-f'（x）=[-2ax+（a+1）]e^x

，h′（x）=（-2ax-a+1）e^x

，（1）当a=0时，h′（x）=e^x＞0对x∈[0，1]恒成立，所以h（x）在[0，1]上单调递增，h（x）max=h（1）=e

（2）当a∈（0，1]时，由h′（x）=0，得x=

1

2a

-

1

2

≥0

①当

1

2a

-

1

2

≥1时，即a∈（0，

1

3

]时，h′（x）≥0对x∈[0，1]恒成立，h（x）在[0，1]上单调递增，h（x）max=h（1）=（1-a）e

②当1＞

1

2a

-

1

2

＞0时，即a∈（

1

3

，1）时，h（x）在[0，

1

2a

-

1

2

）上单调递增，在（

1

2a

-

1

2

，1]上单调递减，h（x）max=h（

1

2a

-

1

2

）=2ae

1-a

2a

③当

1

2a

-

1

2

=0时，即a=1时，h′（x）≤0对x∈[0，1]恒成立，h（x）在[0，1]上单调递减，h（x）max=h（0）=a+1

综上，当a=0时，h（x）max=e，当a∈（0，

1

3

]时，h（x）max=）=（1-a）e

当a∈（

1

3

，1）时，h（x）max=2ae

1-a

2a

，当a=1时，h（x）max=a+1．

（Ⅲ）由（Ⅰ）知，问题可转换为判定方程（x-1）²e^x=x，x＞1的实根的个数．设φ（x）=（x-1）²e^x-x，则φ′（x）=（x²-1）e^x-1，再设k（x）=（x²-1）e^x-1，x＞1，则k′（x）=e^x（x²+2x-1）

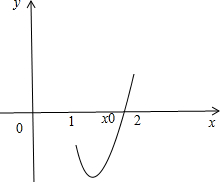
x＞1时，k′（x）＞0，k（x）在（1，+∞）上单调递增，又k（1）=-1＜0，k（2）=3e²-1＞0，所以在（1，2）上存在唯一x₀，使得k（x₀）=0即存在唯一x₀，使得φ′（x₀）=0．

从而φ（x）在（1，x₀）上单调递减，在（x₀，+∞）上单调递增，φ（x₀）＜φ（1）=-1＜0，又φ（2）=e²-2＞0故y=φ（x）的大致图象如图所示．

因此y=φ（x）在（1，+∞）上只能有一个零点．即当x＞1时，f（x）=x只有一个实根．