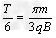问题
计算题
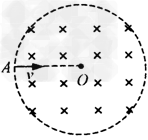
如图所示，分布在半径为r的圆形区域内的匀强磁场，磁感应强度为B，方向垂直纸面向里。电量为q、质量为m的带正电的粒子从磁场边缘A点沿圆的半径AO方向射入磁场，离开磁场时速度方向偏转了60°角。试确定：
（1）粒子做圆周运动的半径。
（2）粒子的入射速度。
（3）若保持粒子的速率不变，从A点入射时速度的方向顺时针转过60°角，粒子在磁场中运动的时间。
答案
解：（1）设带电粒子在匀强磁场中做匀速圆周运动半径为R，如图所示，∠OO'A = 30°，由图可知，圆运动的半径R= O'A =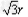 
（2）根据牛顿运动定律， 有：Bqv = m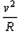
有：R = 
故粒子的入射速度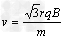
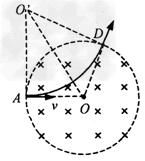
（3）当带电粒子入射方向转过60°角，如图所示，在△OAO1中，OA= r，O1A=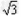 
r，∠O1AO=30°，由几何关系可得，O1O=r，∠AO1E=60°
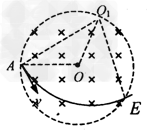
设带电粒子在磁场中运动所用时间为t，由：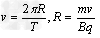
有：T =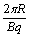 
解出：t = 