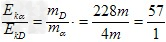解：(1)静止的原子核A发生衰变时，系统的总动量守恒，

由此可知放出的粒子C与产生的新原子核D的动量大小相等．

设粒子C的质量为m_C，速率为v_C，新原子核D的质量为m_D，速率为v_D，

则有m_Cv_C=m_Dv_D        ①    

若粒子C与新原子核D的速度方向与磁场方向垂直，

洛伦兹力提供了它们在匀强磁场中做匀速圆周运动的向心力，

根据洛伦兹力公式和向心力公式，

带电粒子在匀强磁场中做匀速圆周运动的轨道半径为

          ②    

由①②两式可知，粒子C与新原子核D的轨道半径跟它们的电荷量成反比，

设粒子C的轨道半径为R_C，电荷量为q_C；

新原子核_D的轨道半径为R_D，电荷量为q_D，

则有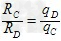          ③    

根据③式可知，电荷量较小的粒子C沿半径大的圆形径迹运动，电荷量较大的新原子核D沿半径小的圆形径迹运动．    

设磁场方向垂直纸面向外，若原子核A发生的是α衰变，放出的粒子C为α粒子，α粒子与新原子核D在匀强磁场中做匀速圆周运动的情形如左图所示；若原子核A发生的是β衰变，放出的粒子C为电子，电子与新原子核D在匀强磁场中做匀速圆周运动的情景如图所示，若磁场方向垂直纸面向里，发生α衰变时类似左图所示，发生β衰变时类似右图所示。  

综合上面的分析可知，原子核A发生的是α衰变，放出的α粒子沿半径大的圆形径迹运动，产生的新原子核D沿半径小的圆形径迹运动．    

(2)设原子核A的电荷数为Z，根据α衰变的法则，新原子核D的电荷数为Z^-2，其电荷量q_D=(Z^-2)e，α粒子的电荷量q_α=2e，

由③式得，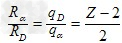

依题意有，解得Z= 90.    

根据原子核中的质子数等于它的电荷数可知，原子核A中有90个质子．    

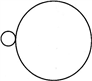
(3)设中子与质子的质量均为m，根据α衰变的法则，新原子核D的质量数为232 -4= 228，其质量m_D= 228m，α粒子的质量m_α=4m，

根据动能与动量大小的关系式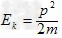和①式可知，

α粒子与新原子核D的动能之比为