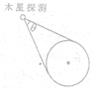
“伽利略”木星探测器，从1989年10月进入太空起，历经6年，行程37亿千米，终于到达木星周围．此后在t秒内绕木星运行N圈后，对木星及其卫星进行考察，最后坠入木星大气层烧毁．设这N圈都是绕木星在同一个圆周上运行，其运行速率为V，探测器上的照相机正对木星拍摄到整个木星时的视角为θ（如图所示），设木星为一球体．   

求：（1）木星探测器在上述圆形轨道上运行时的轨道半径；

（2）若人类能在木星表面着陆，至少以多大的速度将物体从其表面水平抛出，才不至于使物体再落回木星表面．