问题
计算题
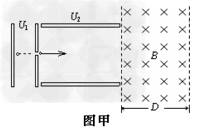
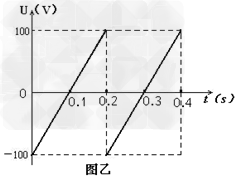
如图甲所示，一个质量为m =2.0×10－11 kg，电荷量q = +1.0×10－5 C的带电微粒（重力忽略不计），从静止开始经U1=100V电压加速后，水平进入两平行金属板间的偏转电场，偏转电场的电压如图乙所示。金属板长L=20cm，两板间距d =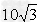
cm。求：
（1）微粒射出偏转电场时的最大偏转角θ；
（2）若紧靠偏转电场边缘有一边界垂直金属板的匀强磁场，该磁场的宽度为D=10cm，为使微粒无法由磁场右边界射出，该匀强磁场的磁感应强度B应满足什么条件？
（3）试求在上述B取最小值的情况下，微粒离开磁场的范围。
答案
解：（1）微粒在加速电场中由动能定理得：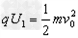
①
解得v0＝1.0×104m/s
微粒在偏转电场中运动的时间为：
因此微粒在偏转电场中运动可认为电场恒定
微粒在偏转电场中做类平抛运动，有：
，
飞出电场时，速度偏转角的正切为：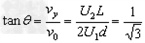
②
解得θ＝30°
（2）进入磁场时微粒的速度是： ③
轨迹如图，由几何关系有：
④
洛伦兹力提供向心力：
⑤
由③～⑤联立得：
代入数据解得：B＝
/5＝0.346T
所以，为使微粒不会由磁场右边射出，该匀强磁场的磁感应强度B至少为0.346T。
（3）设微粒从左边界N处离开，N距轴线与磁场边界交点O的距离为x，有：
可见，在B取最小值时，x仅与U2有关。代入数值可得：X∈【
】
