已知函数f(x)=x3-3x.
(1)求曲线y=f(x)在点x=2处的切线方程;
(2)若过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
(1)f'(x)=3x2-3,f'(2)=9,f(2)=23-3×2=2(2分)
∴曲线y=f(x)在x=2处的切线方程为y-2=9(x-2),即9x-y-16=0(4分)
(2)过点A(1,m)向曲线y=f(x)作切线,设切点为(x0,y0)
则y0=x03-3x0,k=f'(x0)=3x02-3.
则切线方程为y-(x03-3x0)=(3x02-3)(x-x0)(6分)
将A(1,m)代入上式,整理得2x03-3x02+m+3=0.
∵过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线
∴方程2x3-3x2+m+3=0(*)有三个不同实数根、(8分)
记g(x)=2x3-3x2+m+3,g'(x)=6x2-6x=6x(x-1)、
令g'(x)=0,x=0或1、(10分)
则x,g'(x),g(x)的变化情况如下表
| x | (-∞,0) | 0 | (0,1) | 1 | (1,+∞) |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | 递增 | 极大 | 递减 | 极小 | 递增 |
由题意有,当且仅当
,即g(0)>0 g(1)<0
,-3<m<-2时,m+3>0 m+2<0
函数g(x)有三个不同零点、
此时过点A可作曲线y=f(x)的三条不同切线.故m的范围是(-3,-2)(14分)

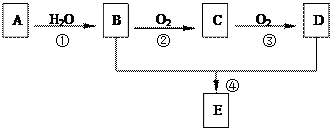
 平②2CH3CHO+O2
平②2CH3CHO+O2 2CH3COOH。现以A为主要原料合成E,E是一种有香味的有机物,其合成路
2CH3COOH。现以A为主要原料合成E,E是一种有香味的有机物,其合成路 线如下图所示。
线如下图所示。