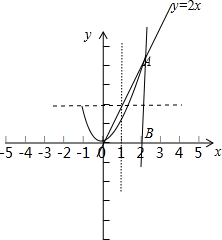
∵（1，2）为曲线f（x）=x³-x²+x+1上的点，设过点（1，2）处的切线的斜率为k，

则k=f′（1）=（3x²-2x+1）|_x=1=2，

∴过点（1，2）处的切线方程为：y-2=2（x-1），即y=2x．

∴y=2x与函数g（x）=x²围成的图形如图：

由

y=2x y=x2

得二曲线交点A（2，4），

又S_△AOB=

1

2

×2×4=4，g（x）=x²围与直线x=2，x轴围成的区域的面积S=

∫

20

x²dx=

x3

3

|

20

=

8

3

，

∴y=2x与函数g（x）=x²围成的图形的面积为：S′=S_△AOB-S=4-

8

3

=

4

3

．

故答案为：

4

3

．