问题
填空题
直线y=a与函数f（x）=x3-3x的图象有相异的三个公共点，则a的取值范围是______．
答案
令f′（x）=3x2-3=0，
得x=±1，
可求得f（x）的极大值为f（-1）=2，
极小值为f（1）=-2，
如图所示
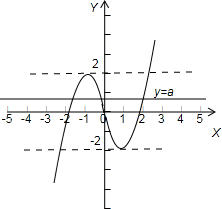
，当满足-2＜a＜2时，恰有三个不同公共点．
故答案为：（-2，2）
搜题请搜索小程序“爱下问搜题”
直线y=a与函数f（x）=x3-3x的图象有相异的三个公共点，则a的取值范围是______．
令f′（x）=3x2-3=0，
得x=±1，
可求得f（x）的极大值为f（-1）=2，
极小值为f（1）=-2，
如图所示
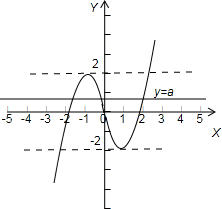
，当满足-2＜a＜2时，恰有三个不同公共点．
故答案为：（-2，2）