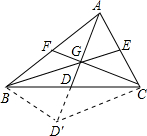
如图，AD、BE、CF为三角形的三条中线，不妨设CF=3，BE=4，AD=5，

延长GD至D′，使DD′=GD，

∵BD=DC，

∴四边形BGCD′是平行四边形，

根据中线的交点性质可知，CG=

2

3

CF=2，D′C=BG=

2

3

BE=

8

3

，D′G=

2

3

AD=

10

3

，

由勾股定理的逆定理，得CG²+D′C²=D′G²，

∴S_△GD′C=

1

2

×CG×D′C=

8

3

；

又S_△GD′C=S_△BGC=

1

2

S_?BD′CG

∴S_△ABC=3S_△BGC=3×

8

3

=8．

故答案为：8．