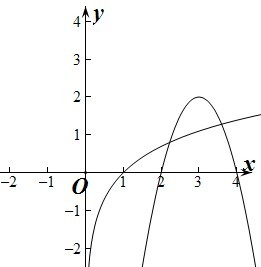
令f（x）=0，得lnx=-2x²+12x-16，设函数f（x）=lnx，g（x）=-2x²+12x-16，

因为g（x）=-2x²+12x-16=-2（x-2）（x-4），

所以x=2，x=4是g（x）=0的两个根，且对称轴为x=3，因为f（3）=ln3＜g（3）=2，在同一个坐标系中分别作出函数

f（x）=lnx，g（x）=-2x²+12x-16的图象如图：

由图象可知函数f（x）=g（x）在区间（2，4）内有两个交点，

所以函数f(x)=

1

2

lnx+x2-6x+8在区间（2，4）内的零点个数是2个．

故选C．