问题
解答题
已知函数f(x)=x3+2x2+x-4,g(x)=ax2+x-8(a>2).
(Ⅰ)求函数f(x)极值;
(Ⅱ)若对任意的x∈[0,+∞)都有f(x)≥g(x),求实数a的取值范围.
答案
(I)f′(x)=3x2+4x+1
令f′(x)=0解得x1=-1或x2=-1 3
当x变化时,f′(x),f(x)的变化情况如下:
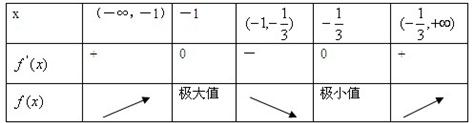
∴当x=-1时,f(x)取得极大值为-4
当x=-
时,f(x)取得极小值为-1 3
;112 27
(Ⅱ)设F(x)=f(x)-g(x)=x3+(2-a)x2+4
∵F(x)≥0在[0,+∞)恒成立⇔F(x)min≥0,
x∈[0,+∞) 且F′(x)=3x2+(4-2a)x
令{F^'}(x)=0,解得x=0,x=2a-4 3
∵a>2,
∴当0<x<
时,F'(x)<02a-4 3
当x>
时,F'(x)>02a-4 3
∴当x∈(0,+∞)时,F(x)min=F(
)≥02a-4 3
即(
)3+(2-a)(2a-4 3
)2+4≥02a-4 3
解得a≤5,
∴2<a≤5
当x=0时,F(x)=4成立
故综上所述:实数a的取值范围是a∈(2,5].
