| 设x=4是函数f(x)=(x2+ax+b)e4-x(x∈R)的一个极值点; (I)求a与b的关系式(用a表示b),并求f(x)的单调区间; (Ⅱ)设a>0,g(x)=(a2+
|
(I)∵f'(x)=(2x+a-x2-ax-b)e4-x=-[x2+(a-2)x+b-a]e4-x
由f'(4)=0,得16+(a-2)4+b-a=0
即b=-3a-8,
∴f(x)=(x2+ax-3a-8)e4-x f′(x)=-[x2+(a-2)x-4a-8]
=-(x-4)(x+a+2)e4-x
令f′(x)=0,得x1=4,x2=-a-2 ∵x=4是f(x)的极值点,故x1≠x2, 即a≠-6 当a<-6时,x1<x2, 故f(x)在(-∞,4]上为减函数,在[4,-a-2]上为增函数,
在[-a-2,+∞)上为减函数.
当a>-6时,x1>x2 故f(x)在(-∞,-a-2]上为减函数,在[-a-2,4]上为增函数
在[4,+∞)上为减函数.
(II)当a>0时,-a-2<0,
∴f(x)在[0,4]上为增函数,在[4,5]上为减函数,
∵f(0)=be4=-(3a+8)e4<0 f(5)=(25+5a-3a-8)e-1=(2a+17)e-1>0
∴f(0)<f(5),
f(4)=16+4a-3a-8=a+8,
∴f(x)在[0,5]上的值域是[-(3a+8)e4,a+8] 而g(x)=(a2+
)2x在[0,5]上为增函数33 4
∴值域为[a2+
,(a2+33 4
)25],33 4
∵(a2+
)-(a+8)=(a-33 4
)2≥0,1 2
若存在ξ1,ξ2∈[0,5]使得|f(ξ1)-g(ξ2)|<4成立.
只要(a2+
)-(a+8)<4,33 4
即(a-
)2<41 2 又a>0∴0<a< 5 2
故a的取值范围是(0,
).5 2

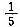 。如果三人一起校对只需6天就可完成。现在如果让乙一人单独校对这份书稿,则需要()天才能完成。
。如果三人一起校对只需6天就可完成。现在如果让乙一人单独校对这份书稿,则需要()天才能完成。