问题
解答题
在直角三角形ABC中,∠A=90°,AD,AE分别是高和角平分线,且△ABE,△AED的面积分别为S1=30,S2=6,求△ADC的面积S.
答案
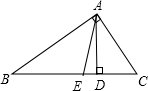
设DE=a,则BE=5a,设CD=xa,只要求出x,根据同底等高三角形面积,6x就是三角形ADC的面积.
(1)由射影定理,AC2=CD?BC,AB2=BD?BC,所以
=AC2 AB2
=CD BD
=xa 6a
①x 6
(2)由角平分线性质,
=AC AB
=CE BE
=xa+a 5a
②x+1 5
(3)联立①②式得到:[
]2=(x+1) 5
这是个一元二次方程,x 6
解得x=
或3 2
.2 3
所以S△ADC=6x=9或4.
故答案为:9或4.
