如图所示,在平行于纸面的平面上建立一个xoy平面直角坐标系,在此坐标系的第一象限内有垂直纸面向里的匀强磁场,磁感应强度为B.一个反质子(质量与质子相同,电荷与质子等值反性)和一个.粒子从坐标原点0垂直磁场方向以相同速度v进入磁场中,速度方向与x轴夹角为30°.已知,反质子的质量为m,带电量为e且为负电荷,a粒子的质量为4m,带电量为2e.
(1)反质子和a粒子在磁场中运动时间之比是多少?
(2)分别求出这两个粒子射出磁场区时的位置坐标.
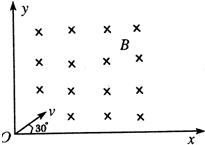
(1)依题知粒子在磁场中受洛伦兹力作用而做匀速圆周运动,设圆周运动半径为R,周期为T,由牛顿第二定律得

qvB=mmv2 R
则得 R=
,T=mv qB
=2πR v 2πm qB
反质子的轨道半径为RP′=
,周期为TP′=mv eB 2πm eB
α粒子的轨道半径为 Rα=
=4mv 2eB 2mv eB
Tα=
=2π?4m 2eB 4πm eB
它们的运动轨迹如图所示,由几何知识知,反质子运动的轨迹对应的圆心角为θ1=60°=π 3
α粒子运动的轨迹对应的圆心角为θ2=120°=2π 3
则反质子在磁场中运动的时间为 tP′=
TP′=1 6
×1 6
=2πm eB mπ 3eB
α粒子在磁场中运动的时间为tα=
Tα=1 3 4πm 3eB
∴反质子和α粒子在磁场中运动时间之比是
=tP′ tα 1 4
(2)反质子和α粒子这两个粒子射出磁场区时的横坐标和纵坐标分别为xP′和yα.
根据几何知识得
xP′=2RP′sin30° yα=2Rα=23 mv eB
∴反质子和α粒子射出磁场区时的位置坐标分别为(
,0)和(0,2mv eB 3
).mv eB
答:
(1)反质子和α粒子在磁场中运动时间之比是
.1 4
(2)反质子和α粒子射出磁场区时的位置坐标分别为(
,0)和(0,2mv eB 3
).mv eB
