问题
问答题
设A为m×n矩阵,且
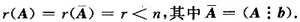
证明方程组AX=b有且仅有n-r+1个线性无关解;
答案
参考答案:令ξ1,ξ2,…,ξn-r为AX=0的基础解系,η0为AX=b的特解,显然β0=η0,β1=ξ1+η0,…,βn-r,=ξn-r+η0为AX=b的一组解,令k0β0+k1β1+…+kn-rβn-r=0,即
k1ξ1+k2ξ2+…+kn-rξn-r+(k0+k1+…+kn-r)η0=0.
上式左乘A得(k0+k1+…+kn-r)b=0,因为b≠0时,k0+k1+…+kn-r=0,于是k1ξ1+k2ξ2+…+kn-rξn-r=0,因为ξ1,ξ2,…,ξn-r,为AX=0的基础解系,所以k1=k2=…-kn-r0,于是k0=0,故β0,β1,…,βn-r线性无关.
若γ0,γ1,…,γn-r+1。为AX=b的线性无关解,则ξ1=γ1-γ0,…,γn-r+1=γn-r+1-γ0为AX=0的解,令k1ξ1+k2ξ2+…+kn-r+1ξn-r+1=0,则
k1γ1+k2γ2+…+kn-r+1γn-r+1-(k1+k2+…+kn-r+1)γ0=0.
因为γ0,γ1,…,γn-r+1件,线性无关,所以k1=k2=…=kn-r+1=0,即ξ1,ξ2,…,ξn-r+1为AX=0的线性无关解,矛盾,故方程组AX=b恰有n-r+1个线性无关解.
