问题
问答题
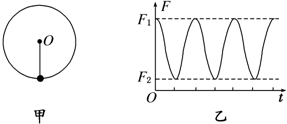
一宇航员到达半径为R、密度均匀的某星球表面,做如下实验:用不可伸长的轻绳拴一质量为m的小球,上端固定在O点,如图甲所示,在最低点给小球某一初速度,使其绕O点在竖直面内做圆周运动,测得绳的拉力大小F随时间t的变化规律如图乙所示.F1、F2已知,引力常量为G,忽略各种阻力.求:
(1)星球表面的重力加速度
(2)星球的密度.
答案
(1)由乙图知:小球做圆周运动在最高点拉力为F2,在最低点拉力为F1.
设最高点速度为v2,最低点速度为v1,绳长为l.
在最高点:F2+mg=
①,m v 22 l
在最低点:F1-mg=
②,m v 21 l
由机械能守恒定律得:
m1 2
=mg•2l+v 21
m1 2
③,g 22
由①②③解得:g=
;④F1-F2 6m
(2)在星球表面:
=mg ⑤GMm R2
星球密度:ρ=
⑥,M V
由⑤⑥解得:ρ=
;F1-F2 8πGmR
答:(1)星球表面的重力加速度为:
.F1-F2 6m
(2)星球的密度为
.F1-F2 8πGmR