问题
问答题
如图所示，在xoy平面内y轴与MN边界之间有沿x轴负方向的匀强电场，y轴左侧和MN边界右侧的空间有垂直纸面向里、磁感应强度大小相等的匀强磁场，MN边界与y轴平行且间距保持不变．一质量为m、电荷量为-q的粒子以速度v0从坐标原点O沿x轴负方向射入磁场，每次经过磁场的时间均为t0，粒子重力不计．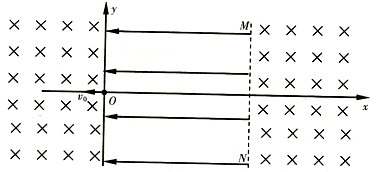
（1）求磁感应强度的大小B．
（2）若t=5t0时粒子回到原点O，求电场区域的宽度d和此时的电场强度E0．
（3）若带电粒子能够回到原点0，则电场强度E应满足什么条件？
答案
粒子在磁场中运动的周期为：T=
…①2πm qB
粒子每次经过磁场时间为半个周期：t0=
…②T 2
由①②解得：B=πm qt0
（2）粒子t=5t0回到原点，轨迹如图，由几何关系知r1=r2
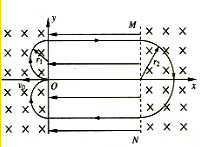根据：qv0B=m v 20 r1
qBv2=mv 22 r2
电场宽度：d=
t0v0+v2 2
解得：d=
t03v0 2
又v2=v0+
t0qE0 m
解得：E0=mv0 qt0
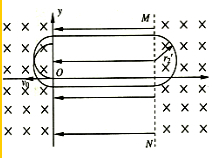（3）如图所示，由几何关系知，要使粒子经过原点，应满足
n（2r
-2r1）=2r1，n=1，2，3，…′2
由：qBv′2=mv ′22 r′2
解得：v′2=
v0n+1 n
根据动能定理知：
Eqd=
m1 2
-v ′22
m1 2 v 20
解得：E=
（n=1，2，3，…）(2n+1)mv0 3n2qt0
答：（1）求磁感应强度的大小为
；πm qt0
（2）若t=5t0时粒子回到原点O，电场区域的宽度d=
t0，此时的电场强度E0=3v0 2
；mv0 qt0
（3）若带电粒子能够回到原点0，则电场强度为
（n=1，2，3，…）．(2n+1)mv0 3n2qt0