问题
问答题
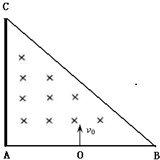
如图所示,等腰直角三角形ABC的区域内有一垂直于纸面向内的匀强磁场,磁感应强度为B,已知AB=2a,现有一束质量为m,带电量为q的正粒子在AB的中点O处沿着垂直与AB的方向以v0打入磁场,在AC边上放置一块足够大的荧光屏,当v0=
时,3aqB m
(1)判断粒子能否打到荧光屏上.
(2)求粒子在磁场中运动的时间.
答案
(1)带电粒子在磁场中做匀速圆周运动,由洛仑兹力提供向心力,有:qv0B=mv 20 R
当:v0=
时,R=3a3aqB m
从0处打入的粒子当轨迹与BC相切时,知该圆轨迹的半径R1(图中虚线所示)满足:R1+a=
R12
得 R1=(
+1)a<R=3a2
所以粒子不能打到荧光屏上
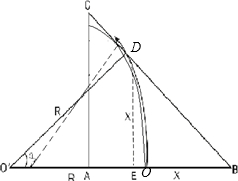
(2)以v0打入的粒子轨迹如图(轨迹半径为图中实线所示),圆心为O′,圆心角为α,从BC边上出射点为D,过D作AB垂线,垂足为E,设DE=x,则有:
R+a=Rsinα+Rcosα
得:sin2α=7 9
α=
arcsin1 2 7 9
运动时间为t=
T=α 2π
?α 2π
=2πm qB
=αm qB marcsin 7 9 2qB
答:
(1)粒子不能打到荧光屏上.
(2)粒子在磁场中运动的时间为
.marcsin 7 9 2qB
