问题
填空题
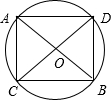
从圆中挖出一个最大的正方形,则正方形的面积与圆的面积之比是______.
答案
设圆的半径为r,
则圆的面积是:s=πr2,
因为,在直角三角形CBD中,
CD2=BC2+BD2,
即,(2r)2=BC2+BD2,
又因为,BC=BD,
所以,4r2=2BC2,
2r2=BC2,
正方形的面积是:s=BC×BD=BC2=2r2,
所以,正方形的面积与圆的面积之比是:2r2:πr2=2:π,
故答案为:2:π.