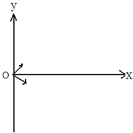
如图所示,在y轴右侧平面内存在方向向内的匀强磁场,磁感应强度B=0、5T,坐标原点O有一放射源,可以向y轴右侧面内沿各个方向放射比荷=4×106C/Kg的正离子,这些正离子的速率分别在零到vmax=2×106m/s的范围内,不计离子之间的相互作用.
(1)求离子打到y轴上的范围
(2)若在某时刻沿+x方向放射各种速率的离子,求经过t=×10-7s时这些离子所在位置构成的曲线方程.
(3)若从某时刻开始向y轴右侧各个方向放射各种速率的离子,求经过t=×10-7s时已进入磁场的离子可能出现的区域面积.
(1)洛伦兹力提供向心力,则有:Bqvm=m
解得:R=1m
则离子打到y轴上的范围为0-2m
(2)由周期公式可得,T==π×10-6s
设这些离子经过t=π×10-7s时,其轨迹所对应的圆心角为 θ.
θ==令t时刻离子所在位置坐标为(x,y),
则x=rsinθ;
y=r(1-cosθ)
y=x(0≤x≤)
(3)t时刻已进入磁场的区域,其面积
为S=πR2+πR2-R×R=(π-)m2
答:(1)求离子打到y轴上的范围为0-2m;
(2)若在某时刻沿+x方向放射各种速率的离子,则经过t=×10-7s时这些离子所在位置构成的曲线方程y=x(0≤x≤)
(3)若从某时刻开始向y轴右侧各个方向放射各种速率的离子,则经过t=×10-7s时已进入磁场的离子可能出现的区域面积为(π-)m2.