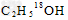如图所示,质量为m.电荷量为e的电子从坐标原点0处沿xOy平面射人第一象限内,射入时的速度方向不同,但大小均为v0.已知包括原点O在内的圆形区域内有方向垂直于xOy平面向里的匀强磁场,磁感应强度大小为B,这些电子穿出磁场后都能垂直打在与y轴平行的荧光屏MN上,屏MN与y轴间的距离等于电子在磁场中做圆周运动的半径的2倍(不计电子的重力以及电子间相互作用).
(1)在O点沿y轴正方向进入磁场的电子经多长时间打在屏上?
(2)若电子穿出磁场时的位置坐标为(x,y),试写出x与y应满足的方程式,并分析指出圆形磁场区的圆心位置坐标和半径;
(3)求这些电子在磁场中运动范围的面积.
(1)设电子做圆周运动的半径为R,
由牛顿第二定律可得,ev0B=m v 20 R
解得:R=mv0 eB
电子做圆周运动的周期:T=2πm eB
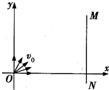
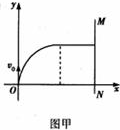
沿y轴正方向进入磁场的电子运动轨迹,如图甲所示.
电子在磁场中运动的时间:t1=
=T 4 πm 2eB
电子穿出磁场后的运动时间:t2=
=2R-R v0 m eB
所以该电子运动的时间:t=t1+t2=(π+2)m 2eB
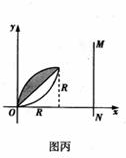
(2)入射方向与x轴正方向夹角为θ的电子轨迹,如图乙所示,
电子穿出磁场时的位置坐标为(x,y),
由图乙可得:x2+(R-y)2=R2,
即x2+(y-
)2=(mv0 eB
)2mv0 eB
电子穿出磁场的位置在磁场圆的圆周上,故磁场圆周圆心坐标为(0,
)mv0 eB
磁场圆半径等于轨迹圆半径为r=R=mv0 eB
磁场圆如图乙所示中虚线圆所示.
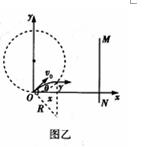
(3)这些电子在磁场中的运动范围由图丙所示的两段圆弧围成,
面积等于图中阴影面积的2倍,即:S=2•(
-πR2 4
)=R2 2
(π-2 2
)2mv0 eB
答:
(1)在O点沿y轴正方向进入磁场的电子经
时间打在屏上;(π+2)m 2eB
(2)若电子穿出磁场时的位置坐标为(x,y),则x与y应满足的方程式,并分析指出圆形磁场区的圆心位置坐标(0,
)和半径mv0 eB
;mv0 eB
(3)则这些电子在磁场中运动范围的面积
(π-2 2
)2.mv0 eB

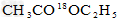 的水解产物是
的水解产物是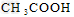 和
和