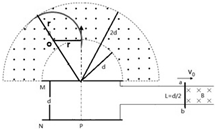
如图a,间距为d的平行金属板MN与一对光滑的平行导轨相连,平行导轨间距L=
,一根导体棒ab以一定的初速度向右匀速运动,棒的右端存在一个垂直纸面向里,磁感应强度大小为B的匀强磁场.棒进入磁场的同时,粒子源P释放一个初速度为零的带电粒子,已知带电粒子质量为m,电荷量为q,粒子能从N板加速到M板,并从M板上的一个小孔穿出.在板的上方,有一个环形区域内存在磁感应强度大小也为B,垂直纸面向外的匀强磁场.已知外圆半径为2d,内圆半径为d,两圆的圆心与小孔重合(粒子重力不计).d 2

(1)判断带电粒子的正负,并求当ab棒的速度为v0时,粒子到达M板的速度v;
(2)若要求粒子不能从外圆边界飞出,则ab棒运动速度v0的取值范围是多少?
(3)若棒ab的速度
=v ′0
,为使粒子不从外圆飞出,可通过控制导轨区域磁场的宽度S(如图b),则该磁场宽度S应控制在多少范围内?qBd m
(1)根据右手定则知,a端为正极,故带电粒子必须带负电
ab棒切割磁感线,产生的电动势U=B
v0d 2
对于粒子,由动能定理qU=
mv2-0 1 2
得粒子射出电容器的速度为 v=qBdv0 m
(2)要使粒子不从外边界飞出,则粒子最大半径时的轨迹与外圆相切,
由几何关系有:(2d-r)2=r2+d2
得 r=
d3 4
由洛仑兹力等于向心力,有:qvB=mv 20 r
联立得 v0=9qBd 16m
故ab棒的速度范围:v0≤9qBd 16m
(3)因为
=v ′0
>vm,故如果让粒子在MN间一直加速,则必然会从外圆飞出,qBd m
所以只能让粒子在MN间只加速至速度为 v=
=qBdv0 m
,再匀速射出电容器则可.3qBd 4m
而带电粒子在电场中加速过程,有
a=
=qU md q(Bv0′
)d 2 md
将
=v ′0
代入得:a=qBd m q2B2d 2m2
由v=
=at=3qBd 4m
t q2B2d 2m2
得:t=3m 2qB
对于棒ab:s=v0′t=
d 3 2
故磁场的宽度应:s≤
d 3 2
答:
(1)带电粒子带负电,当ab棒的速度为v0时,粒子到达M板的速度v是
;qBdv0 m
(2)若要求粒子不能从外圆边界飞出,则ab棒运动速度v0的取值范围是:v0≤
.9qBd 16m
(3)若棒ab的速度
=v ′0
,为使粒子不从外圆飞出,可通过控制导轨区域磁场的宽度S(如图b),则该磁场宽度S应控制在qBd m
d之内.3 2
