如图所示,磁感应强度大小为B=0.15T,方向垂直纸面向里的匀强磁场分布在半径R=0.10m的圆形区域内,圆的左端点跟y轴相切于直角坐标系原点O,右端跟荧光屏MN相切于x轴上的A点.置于坐标原点O的粒子源可沿x轴正方向射出速度v0=3.0×106m/s的带电粒子流,比荷为q/m=1.0×108C/kg.不计粒子重力.求:
(1)粒子在磁场中运动的半径;
(2)粒子射到荧光屏MN上的点距A点的距离;
(3)现以O点并垂直于纸面的直线为轴,将圆形磁场逆时针缓慢旋转90°,在答题纸上用作图法画出此过程中粒子打在荧光屏上的最低点和最高点的位置.
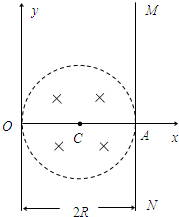
(1)粒子在磁场中作匀速圆周运动,设半径为r,
由牛顿第二定律可得:qv0B=m
,r=v 20 r mv0 qB
代入数据可得:r=0.20m
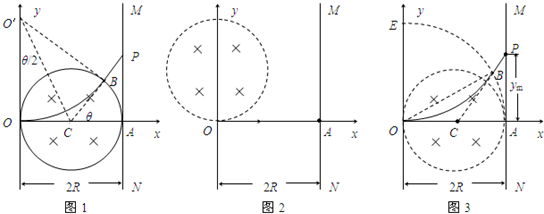
(2)作出粒子运动轨迹如图1所示.粒子在B点射出,磁场中转过的偏向角为θ,由图可得:tan
=θ 2
=0.5R r
由数学知识可得:tanθ=
=2tan θ 2 1-tan2 θ 2 4 3
故PA=Rtanθ=0.1×
m=4 3
m≈0.13m2 15
(3)当圆形磁场区域转过90°时,粒子打在A点,A点即为最低点,如图2所示.
作图说明:以O为圆心、OA为半径作出圆孤AE交y轴于E点,以E为圆心、EO为半径作粒子运动轨迹交AE孤于B点,连接CB并延长交屏于P点,P点即为粒子到达的最高点.
答:(1)粒子在磁场中运动的半径为0.20m;
(2)粒子射到荧光屏MN上的点距A点的距离为0.13m;
(3)当圆形磁场区域转过90°时,粒子打在A点,A点即为最低点,如图2所示.
作图说明:以O为圆心、OA为半径作出圆孤AE交y轴于E点,以E为圆心、EO为半径作粒子运动轨迹交AE孤于B点,连接CB并延长交屏于P点,P点即为粒子到达的最高点.如图3所示.
