问题
解答题
| 已知f(x)是二次函数,不等式f(x)<0的解集是(0,5),且f(x)在点(1,f(1))处的切线与直线6x+y+1=0平行. (1)求f(x)的解析式; (2)是否存在t∈N*,使得方程f(x)+
|
答案
(1)∵f(x)是二次函数,且f(x)<0的解集是(0,5),
∴可设f(x)=ax(x-5)=ax2-5ax,(a>0).
∴f(x)在点(1,f(1))处的切线斜率是:f′(1)=-3a=-6.
∴a=2,∴f(x)=2x(x-5)=2x2-10x(x∈R).
(2)方程f(x)+
=0等价于方程 2x3-10x2+37=0.37 x
设h(x)=2x3-10x2+37,则h'(x)=6x2-20x=2x(3x-10).
在区间x∈(0,
)时,h'(x)<0,h(x)是减函数;10 3
在区间(-∞,0),或(
,+∞)上,h'(x)>0,h(x)是增函数,故h(0)是极大值,h(10 3
)是极小值.10 3
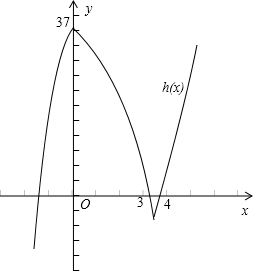
∵h(3)=1>0,h(
)=-10 3
<0,h(4)=5>0,1 27
∴方程h(x)=0在区间(3,
),(10 3
,4)内分别有惟一实数根,故函数h(x)在(3,4)内有2个零点.10 3
而在区间(0,3),(4,+∞)内没有零点,在(-∞,0)上有唯一的零点.
画出函数h(x)的单调性和零点情况的简图,如图所示.
所以存在惟一的正整数t=3,使得方程f(x)+
=0在区间(t,t+1)内有且只有两个不同的实数根.37 x
