如图1,在xoy 平面内有垂直纸面的有界匀强磁场,磁感应强度大小均为B,其中0<x<a区域内磁场方向垂直xoy 平面向里,a<x区域内磁场方向垂直xoy 平面向外,x<0区域内无磁场.一个带正电q、质量为m 的粒子(粒子重力不计)在坐标原点处,以某一初速度沿x轴正方向射入磁场.
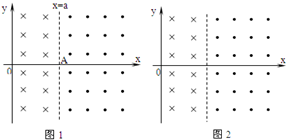
(1)求要使粒子能进入第二个磁场,初速度要满足的条件;
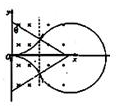
(2)粒子初速度改为v1,要使粒子经过两个磁场后沿x轴负方向经过O点,求图中磁场分界线(图中虚线)的横坐标值为多少?要在图2中画出轨迹图.
(3)在第二问的情况下,要使带电粒子第二次回到O点,且回到O点时的速度方向沿x轴正方向,请在x<0内设计符合要求的磁场,在图2上标明磁场的方向、磁感应强度的大小和边界的坐标?
(4)若粒子在第一个磁场中作圆周运动的轨迹半径为R=
a,求粒子在磁场中的轨迹与x 轴的交点坐标.2
(1)质子在磁场中受到洛伦兹力做匀速圆周运动,
根据牛顿第二定律则有:qvB=m
,v2 R
进入第二个磁场的条件:R>a
初速度满足:v>Bqa m
(2)有对称性分析,右边的圆弧的圆心一定在X轴上,正确画出轨迹图,
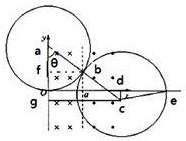
且三段圆弧的圆心正好构成一个正三角形,
所以θ=60° a
点的坐标变为X=R sinθ=
mv03 2Bq
(3)如图所示,
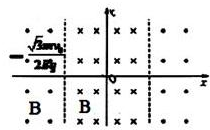
(4)质子在磁场中受到洛伦兹力做匀速圆周运动,
根据牛顿第二定律,有:qvB=m
,v2 R
得质子做匀速圆周运动的半径为:R=
,mv Bq
带电粒子在两个磁场中的半径都为R=
a,2
则有sinθ=
,a R
得到θ=45°,
圆心C的坐标为XC=2Rsinθ=2a
YC=-(2a•R)=-(2-
)a,所以圆方程为(x-2a)2+(y+2a-2
a)2=2a2,2
将y=0代入得,X=2(1+
)a,所以交点坐标为(2(1+
-12
)a,0)
-12
答:(1)求要使粒子能进入第二个磁场,初速度要满足的条件是:v>
;Bqa m
(2)粒子初速度改为v1,要使粒子经过两个磁场后沿x轴负方向经过O点,则图中磁场分界线(图中虚线)的横坐标值为X=
;要在图2中画出轨迹图.
mv03 2Bq
(3)如图所示,
(4)若粒子在第一个磁场中作圆周运动的轨迹半径为R=
a,求粒子在磁场中的轨迹与x 轴的交点坐标为(2(1+2
)a,0).
-12
