问题
问答题
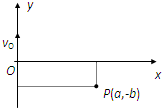
如图所示,在直角坐标系xOy内,有一质量为m,电量为+q的电荷从原点O点沿y轴正方向以初速度v0出发,电荷重力不计,现要求电荷能通过P点(a,-b),|a|>|b|,速度的大小不变.为了满足上述要求,需在电荷运动的空间范围内加上一个垂直于纸面的匀强磁场,试设计三种不同强度和空间区域的磁场以满足题中的要求.(说明:粒子过P点时速度的方向可以是任意的,但在xoy平面内)
答案
方案(1):磁场方向垂直纸面向外,
粒子在从O运动到P的整个运动过程均处于磁场中如下图;由几何关系可知:
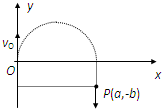
有:
=a a2+b2 a2+b2 2R
得:R=a2+b2 2a
由:R=
,mv qB
得:B=2mva q(a2+b2)
方案(2):磁场方向垂直纸面向外
磁场只存在于x轴上方,运动轨道如右图所示:
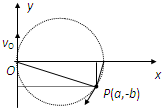
由几何关系可知:R=a 2
R=
;mv qB
得:B=2mv qa
方案(3):磁场方向垂直纸面向里
如果粒子的运动半径正好等于b,且磁场区域只存在于EF的左上方,EF与x轴成450,则即可达到题中的要求:
由R=mv qB
得B=mv qb
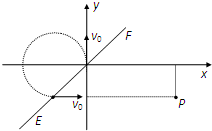
答:三种方案如上.
