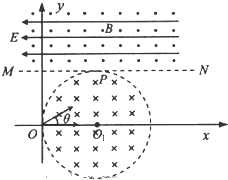
如图所示,方向垂直纸面向里的匀强磁场的边界,是一个半径为r的圆,圆心O1在x轴上,OO1距离等于圆的半径.虚线MN平行于x轴且与圆相切于P点,在MN的上方是正交的匀强电场和匀强磁场,电场强度的大小为E,方向沿x轴的负方向,磁感应强度为B,方向垂直纸面向外.有-群相同的正粒子,以相同的速率,在纸面内沿不同方向从原点O射入第I象限,粒子的速度方向在与x轴成θ=30°角的范围内,其中沿x轴正方向进入磁场的粒子经过P点射入MN后,恰好在正交的电磁场中做直线运动.粒子的质量为m.电荷量为q(不计粒子的重力).求:
(1)粒子的初速率;
(2)圆形有界磁场的磁感应强度:
(3)若只撤去虚线MN上面的磁场B,这些粒子经过y轴的坐标范围.
(1)带电粒子受到电场力与洛伦兹力相平衡,
则有:qE=qv0B
解得:v0=E B
(2)设正粒子在圆形有界磁场中做匀速圆周运动的半径为R,
则有:R=r
洛伦兹力提供向心力,根据牛顿第二定律,
则有:B′qv0=
,m v 20 R
解得:B′=mE qBr
(3)沿x轴正方向进入圆形有界磁场的粒子经电场E偏转后,过y轴上点的坐标最大,
则有:r=1 2
t2 qE m
且△y1=v0t1
所以 y1=△y1+r
解得:y1=r+E B 2mr Eq
沿与x轴正方向与θ=30°角进入圆形有界磁场的粒子经电场E偏转后,过y轴上点的坐标最小,
则有:
=r 2 1 2 qE m t 22
又△y2=v0t2
且 y2=△y2+r
解得:y2=r+E B mr Eq
即,r+E B
≤y≤r+mr Eq E B 2mr Eq
答:(1)粒子的初速率
;E B
(2)圆形有界磁场的磁感应强度
:mE qBr
(3)若只撤去虚线MN上面的磁场B,这些粒子经过y轴的坐标范围r+E B
≤y≤r+mr Eq E B
.2mr Eq
