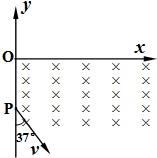
如图所示,在平面直角坐标系xoy的第四象限有垂直纸面向里的匀强磁场,一质量为m=5.0×10-8kg、电量为q=1.0×10-6C的带电粒子,从静止开始经U0=10V的电压加速后,从P点沿图示方向进入磁场,已知OP=30cm,(粒子重力不计,sin37°=0.6,cos37°=0.8),求:
(1)带电粒子到达P点时速度v的大小
(2)若磁感应强度B=2.0T,粒子从x轴上的Q点离开磁场,求QO的距离
(3)若粒子不能进入x轴上方,求磁感应强度B'满足的条件.
(1)对带电粒子的加速过程,由
动能定理qU=
mv21 2

代入数据得:v=20m/s
(2)带电粒子仅在洛伦兹力作用下做匀速圆周运动,
有:qvB=mv2 R
得R=mv qB
代入数据得:R=0.50m
而
=0.50m OP cos53°
故圆心一定在x轴上,轨迹如图所示.
由几何关系可知:OQ=R+Rsin53°
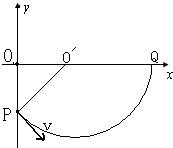
故OQ=0.90m
(3)带电粒子不从x轴射出(如图),
由几何关系得:OP>R'+R'cos53°①
R′=
②mv qB′
由①②并代入数据得:B'>
T=5.33T 16 3
答:(1)带电粒子到达P点时速度v的大小20m/s;
(2)若磁感应强度B=2.0T,粒子从x轴上的Q点离开磁场,则QO的距离0.9m;
(3)若粒子不能进入x轴上方,则磁感应强度B'满足大于5.33T条件.
