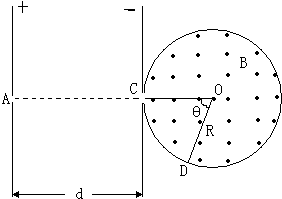
在光滑绝缘的水平桌面上，有两个质量均为m，电量为+q的完全相同

问题问答题

在光滑绝缘的水平桌面上，有两个质量均为m，电量为+q的完全相同的带电粒子P₁和P₂，在小孔A处以初速度为零先后释放．在平行板间距为d的匀强电场中加速后，P₁从C处对着圆心进入半径为R的固定圆筒中（筒壁上的小孔C只能容一个粒子通过），圆筒内有垂直水平面向上的磁感应强度为B的匀强磁场．P₁每次与筒壁发生碰撞均无电荷迁移，P₁进入磁场第一次与筒壁碰撞点为D，∠COD=θ，如图所示．延后释放的P₂，将第一次欲逃逸出圆筒的P₁正碰圆筒内，此次碰撞刚结束，立即改变平行板间的电压，并利用P₂与P₁之后的碰撞，将P₁限制在圆筒内运动．碰撞过程均无机械能损失．设d=

πR，求：在P₂和P₁相邻两次碰撞时间间隔内，粒子P₁与筒壁的可能碰撞次数．

附：部分三角函数值

2π

tanφ

3.08

1.73

1.00

0.73

0.58

0.48

0.41

0.36

0.32

答案

粒子在磁场中匀速圆周运动的周期T=

2πm

，

由几何知识，得半径r=Rtan

从C到D的时间t_CD=

π-θ

2π

P₁、P₂每次碰撞都应当在C点．

设P₁在圆筒内转动了n圈和筒壁碰撞了K次后与P₂相碰于C点，则K+1=

2πn

所以两粒子每次碰撞的时间间隔t=t_CD（K+1）=

2πm

•

π-θ

2π

(k+1)=

m(π-

2πn

k+1

)

(k+1)

在t 时间内，P₂向左运动x再回到C，平均速度为

t=2

≤

5πR

由上述两式可得，

5πR

≥

m(π-

2πn

k+1

)

(k+1)

（k+1）

(1-

k+1

)≤

tan

nπ

k+1

(k+1-2n)≤

当 n=1，K=2、3、4、5、6、7 时符合条件，K=1、8、9…不符合条件

当 n=2，3，4…．时，无论K等于多少，均不符合条件．

答：在P₂和P₁相邻两次碰撞时间间隔内，粒子P₁与筒壁的可能碰撞次数为2、3、4、5、6、7．