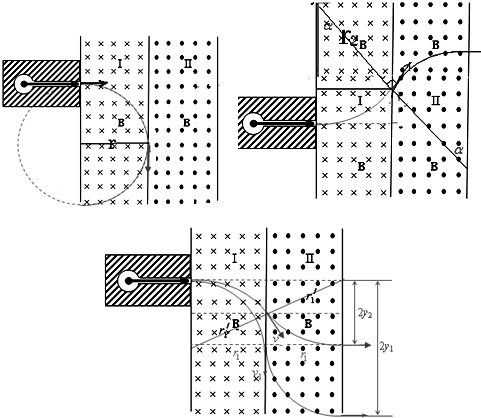
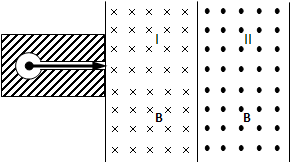
有一个放射源水平放射出A、B两种粒子,垂直射入如图所示磁场区域Ⅰ中.区域Ⅰ和Ⅱ的宽度均为d,长度足够长,各自存在着垂直纸面的匀强磁场,两区域的磁感强度大小B相等,方向相反(粒子运动不考虑相对论效应).已知A粒子带负电,电量为q、质量为m;B粒子带正电,电量为2q、质量为4m.
(1)若要使A粒子能够进入区域Ⅱ,求A粒子的初速度v1的最小值;
(2)B粒子射出初速度大小v2=
,计算B粒子在区域Ⅰ和Ⅱ中运动的总时间;Bqd m
(3)当v1满足第(1)小题所给值时,请求出速率在
v1>v>v1区间的B粒子离开区域Ⅱ时的区域宽度和方向.5 3
(1)作出临界轨道,对A粒子刚好能够进入区域Ⅱ时,初速度v1的最小值
由几何关系知r1=d,又Bqv1=m
得 v1=v 21 r1 Bqd m
(2)对B粒子B2qv1=4mv 22 r2
得r2=2d
则sinα=
=d 2d
,α=1 2
T=π 6
=2π4m B2q 4πm bq
故t总=
T=1 6 2πm 3Bq
(3)画出速率分别为v1和v2的粒子离开区域Ⅱ轨迹如下图
当v=v1时,r1=d,粒子向下侧移y1=d
当v=
v1时,5 3
=r /1
=m.
v15 3 Bq
d,粒子向下侧移y2=r′-5 3
=r
-d2′ 21 d 3
故B粒子离开区域Ⅱ时的区域△y=2y1-2y2=
d4 3
方向都与磁场区域Ⅱ右边界垂直
答:(1)A粒子的初速度v1的最小值v1=
.Bqd m
(2)B粒子在区域Ⅰ和Ⅱ中运动的总时间t总=
;2πm 3Bq
(3)B粒子离开区域Ⅱ时的区域宽度为
d,方向都与磁场区域Ⅱ右边界垂直. 4 3