问题
问答题
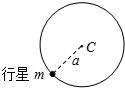
太阳系以外存在着许多恒星与行星组成的双星系统.它们运行的原理可以理解为,质量为M的恒星和质量为m的行星(M大于m),在它们之间的万有引力作用下有规则地运动着.如图所示,我们可认为行星在以某一定点c为中心、半径为a的圆周上做匀速圆周运动(图中没有表示出恒星).设万有引力常量为G,恒星和行星的大小可忽略不计.
(1)试在图中粗略画出恒星运动的轨道和位置;
(2)试计算恒星与点c间的距离和恒星的运行速率v.
答案
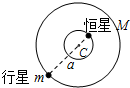
(1)两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,故两恒星运动的轨道和位置大致如图:
(2)对行星m,F=mω2Rm----------①
对恒星M,F′=mω2RM------------②
根据牛顿第二定律,F与F′大小相等
由①②得RM=
Rm=m M
am M
对恒星M,G
=MMm (Rm+RM)2 v2 RM
代入数据解得:v=m m+M GM a
答:(1)恒星运动的轨道和位置大致如上图.
(2)恒星与点c间的距离为
a,恒星的运行速率为m M m m+M
.GM a
