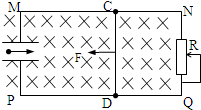
如图所示,两互相平行的水平金属导轨MN、PQ放在竖直平面内,相距为L=0.4cm,左端接平行板电容器,板间距离为d=0.2m,右端接滑动变阻器R(R的最大阻值为Ω),整个空间有水平匀强磁场,磁感应强度为B=10T,方向垂直于导轨所在平面.导体棒CD与导轨接触良好,棒的电阻为r=1Ω,其它电阻及摩擦均不计,现对导体棒施加与导轨平行的大小为F=2N的恒力作用,使棒从静止开始运动,取g=10m/s2.求:
(1)当滑动变阻器R接入电路的阻值最大时,拉力的最大功率是多大?
(2)当滑动触头在滑动变阻器中点且导体棒处于稳定状态时,一带电小球从平行板电容器左侧沿两极板的正中间射入,在两极板间恰好做匀速直线运动;当滑动触头在滑动变阻器最下端且导体棒处于稳定状态时,该带电小球以同样的方式和速度入射,在两极间恰能做匀速圆周运动,求圆周的半径是多大?
(1)当棒达到匀速运动时,金属棒受到的安培力:
FB=BIL=B
L=BLv R+r
,B2L2v R+r
由平衡条件得:F=FB,即:F=
,B2L2v R+r
导体棒的速度v=
,F(R+r) B2L2
拉力功率P=Fv=F2(R+r) B2L2
可知,回路的总电阻越大时,拉力功率越大,当R=2Ω时,拉力功率最大,最大功率为Pm=0.75W;
(2)当触头滑到中点即R=1Ω时
棒匀速运动的速度v1=
=0.25m/sF(R+r) B2L2
导体棒产生的感应电动势E1=BLv1=10×0.4×0.25=1V
电容器两极板间电压U1=
=0.5V,E1R R+r
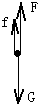
由于棒在平行板间做匀速直线运动,则小球必带正电
此时小球受力情况如图所示,设小球的入射速度为v0
由平衡条件知:F+f=G 即 q
+qv0B=mg…①U1 d
当滑头滑至下端即R=2Ω时,棒的速度v2=
=F(R+r) B2L2
m/s3 8
导体棒产生的感应电动势 E2=BLv2=1.5V
电容器两极板间的电压U2=
=1VE2R R+r
由于小球在平行板间做匀速圆周运动
电场力与重力平衡,于是:q
=mg…②U2 d
代入数值,由①②解得:v0=
=0.25m/sU2-U1 Bd
小球作圆周运动时洛仑兹力提供向心力
由牛顿第二定律得:qv0B=mv 20 r
小球作圆周运动的半径为r=0.0125m
答:
(1)导体棒处于稳定状态时拉力的最大功率是0.75W.
(2)小球在两极板间恰好做匀速圆周运动的速度为0.25m/s,做圆周运动的轨道半径为0.0125m.
