问题
问答题
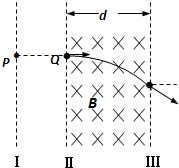
如图所示,Ⅰ、Ⅱ、Ⅲ为电场和磁场的理想边界,一束电子(电量为e,质量为m,重力不计)由静止状态从P点经过Ⅰ、Ⅱ间的电场加速后垂直到达边界Ⅱ的Q点.匀强磁场的磁感应强度为B,磁场边界宽度为d,电子从磁场边界Ⅲ穿出时的速度方向与电子原来的入射方向夹角为30°.求:
(1)电子在磁场中运动的时间t;
(2)若改变PQ间的电势差,使电子刚好不能从边界Ⅲ射出,则此时PQ间的电势差U是多少?
答案
(1)由evB=mv2 R
且T=2πR v
得电子在磁场中运动周期T=2πm eB
电子在磁场中运动时间t=
T=30° 360° T 12
解得:t=πm 6eB
(2)电子刚好不从边界Ⅲ穿出时轨迹与边界相切,运动半径为R=d
由evB=
得mv2 R
v=eBd m
PQ间电场力做功等于动能的增加,由eU=
mv21 2
得U=
;eB2d2 2m
答:(1)电子在磁场中运动的时间t=
;(2)若改变PQ间的电势差,使电子刚好不能从边界Ⅲ射出,则此时PQ间的电势差U=πm 6eB
.eB2d2 2m
