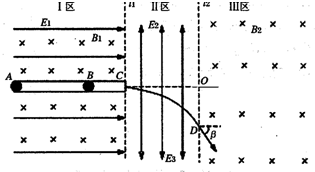
如图所示,虚线 lll2、将无重力场的空间分成三个区域,I 区内存在水平向右的匀强电场E和垂直纸面向里的匀强磁场Bl,Ⅱ区内以水平线 CO 为分界,上方存在着竖直向上的匀强电场E2,下方存在着竖直向下的匀强电场E3Ⅲ区内存在以l2为左边界、右边无界的垂直纸面向里的匀强磁场B2,在 I 区内有一段粗糙、长为 L 的水平放置塑料直管道 AC,一可视为质点的带正电小球(直径比管内径略小)的质量为 m、带电量为 q,现将小球从管道内 A 处由静止释放,运动至管道内离 A 点距离为 L0 的 B 点处时达到稳定速度 v0,后进入Ⅱ区向下偏转,从边界l2上的 D 点进入Ⅲ区,此时速度方向与水平方向的夹角为β,最后小球恰能无碰撞的从 C处进入管道.已知:
=0.01C/kg,E1=l00N/C,E2=E3=300N/C,β=600,Bl=103T,L=5m L 0=4m小球与管道间动摩擦因数为μ=0.1,求:q m
( l )小球在管道内运动的稳定速度 v0 值;
( 2 )Ⅲ区内匀强磁场 B2的值;
( 3 )从 A 处开始至从 C 处进入管道的过程中,小球的运动时间t.
(1)小球在管道内达到稳定速度时,合力为零,在水平方向上有:
qE1=μqv0B1
解得:v0=
=E1 μB1
=1m/s100 0.1×103
(2)小球在从C到D的过程中,做类平抛运动,设加速度为a,在D点时竖直方向上的分速度为vy,OD间的距离为d,在D点时,速度关系为:
tanβ=vy v0
代入数据解得:
vy=
m/s3
在竖直方向上,由运动学公式有:
=2adv 2y
由牛顿运动定律有:
qE3=ma
以上两式联立并代入数据得:
d=0.5m
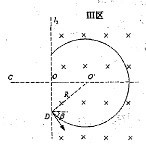
根据题意,为保证小球能无碰撞的从C处进入管道,小球在Ⅲ区内做匀速圆周运动的圆弧是关于CO对称的,圆心O'必在CO的延长线上.(如图所示)
由几何关系得:
R=
=d sin30°
=1m0.5 0.5
vD=
=2m/s
+v 20 v 2y
小球在Ⅲ区内做匀速圆周运动的向心力是洛伦兹力,有:
qvDB2=mv 2D R
代入数据解得:
B2=200T
(3)小球从A点至B点的过程做变加速直线运动,设小球从A运动至B点所需要的时间为t1,由牛顿第二定律得:
qE1-μqvB1=m△v △t
由动量定理有:
∑(qE1△t)-∑(μqvB1△t)=∑(m△v)
即为:qE1t1-μqB1L0=mv0
带入数据解得:t1=5s
小球从B匀速运动到C所需的时间为:
t2=
=L-L0 v0
=1s5-4 1
小球在Ⅱ区的运动总时间为:
t3=
=1.15s2vy a
小球在Ⅲ区内运动时间为:
t4=
T=5 6
=2.62s5πm 3qB2
则小球从A处开始至从C处进入管道的过程中,运动时间t为:
t=t1+t2+t3+t4=9.77s
答:(1)小球在管道内运动的稳定速度为1m/s.
(2)Ⅲ区内匀强磁场 B2的值为200T.
(3)从 A 处开始至从 C 处进入管道的过程中,小球的运动时间为9.77s.
