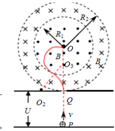
如图所示,有一半径为R1=1m的圆形磁场区域,圆心为O,另有一外半径为R2=U2=U1-U损=1900Vm、内半径为R1的同心环形磁场区域,磁感应强度大小均为B=0.5T,方向相反,均垂直于纸面.一带正电的粒子从平行极板下板P点静止释放,经加速后通过上板小孔Q,垂直进入环形磁场区域,已知点P、Q、O在同一竖直线上,上极板与环形磁场外边界相切,粒子比荷q/m=4×107C/kg,不计粒子的重力,且不考虑粒子的相对论效应.求:
(1)若加速电压U1=1.25×102V,则粒子刚进入环形磁场时的速度v0为多大?
(2)要使粒子不能进入中间的圆形磁场区域,加速电压U2应满足什么条件?
(3)若改变加速电压大小,可使粒子进入圆形磁场区域,且能水平通过圆心O,最后返回到出发点,则粒子从Q孔进入磁场到第一次经过O点所用的时间为多少?
(1)在电场中加速由动能定理知:qU1=
m1 2
,v 20
解得:v0=1×105m/s.
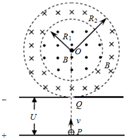
(2)粒子刚好不进入中间磁场时,如图,有几何知识知:
+r 21
=(r1+R1)2,R 22
其中r1=
=1m,mv qB
又qU2=
m1 2
,要是粒子不能进入中间的圆形磁场区域v 2
电压满足:U2≤5×106V.
(3)轨迹如图,在磁场中运动时间为:
t=(
+1 6
)T=5 12
T≈1.83×10-7s.7 12
答:(1)粒子刚进入环形磁场时的速率为1×105m/s;
(2)要使粒子能进入中间的圆形磁场区域,加速电压U2应满足条件:U2≤5×106V;
(3)粒子从Q孔进人磁场到第一次回到Q点所用的时间约为1.83×10-7s.