问题
选择题
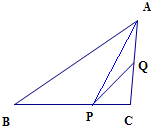
在△ABC中,点P在BC上,且
|
答案
设C坐标为(x,y),
∵P为坐标原点,∴
=(x,y),PC
∵△PAC中,Q为AC中点,∴
=PQ
(1 2
+PA
),PC
结合
=(4,3),PA
=(1,5),可得PQ
,解之得x=-2,y=7.1=
(4+x)1 2 5=
(3+y)1 2
∴
=(-2,7),可得PC
=2BP
=(-4,14),PC
因此,
=BC
+BP
=(-6,21),PC
故选:D