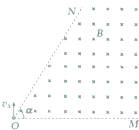
如图所示,在以OM和ON为边界的区域内有一磁感应强度为B,垂直于纸面向里的匀强磁场,在ON的左侧区域存在一平行于OM的匀强电场(图中未画出),OM、ON间的夹角α满足tanα=,现有大量的带负电的粒子从O点以大小不同的速度垂直射入电场,粒子在MON平面内运动,一段时间后通过ON边界进入磁场,已知带电粒子的质量为m,带电量为q,以v0的初速度射入电场中的粒子在磁场中运动时恰好与OM边界相切.不计重力和粒子间的相互作用,tan37°=
(1)试确定这些带电粒子第一次进入磁场的方向;
(2)试确定匀强电场的电场强度的大小和方向;
(3)若带电粒子射入电场的初速度vx≥v0 ,试确定这些带电粒子第一次在磁场中运动的时间范围.(可用反三角函数表示)
(1)以O为坐标原点,vx方向为想轴,OM方向为y轴建立直角坐标系如图所示,
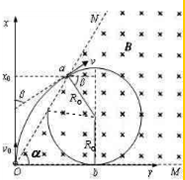
粒子在电场中做类平抛运动,
在x轴方向上:x=vxt,在y轴方向上:y=at2,
tanα=,tanβ==,
解得:tanβ==,则β=53°,
所用带电粒子进入磁场的速度方向均与初速度方向成53°角.
(2)由题意可知,电场方向平行于OM向左,
由(1)所列方程可解得:t=,x==,
带电粒子进入磁场做匀速圆周运动,
由牛顿第二定律得:qvB=m ①,
解得:R===,
以v0的速度射入电场中的粒子在电磁场中的运动轨迹如图中实线所示,
由几何知识可知,x0=R0(1+sinβ)=R0 ②,
将v0代入①②解得:a=,
而a=,解得:E=;
(3)由图示可知,粒子进入磁场的位置点a到粒子在磁场中做圆周运动的圆弧最低点b在x轴方向上的距离d为:
d=R(1+sinβ)=,
则有:=,可知:当vx<v0时,粒子将从OM边界飞出,
可知当vx>v0时,粒子将不能从OM边界飞出,
因此当带电粒子的速度vx=v0时,粒子第一次在磁场中的运动时间最短,
此时粒子进入磁场时沿x方向的位移与粒子在磁场中做圆周运动的半径关系为=,则圆心恰好在OM上,如图所示:
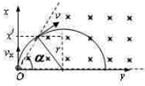
由图示可知,带电粒子在磁场中运动的最短时间:
tmin=T=×=,
故当带电粒子带电速度vx≥v0时,粒子第一次在磁场中运动的时间相同且最长,
由图示可知,最长时间:tmax=T=,其中:α=arctan,β=arctan,
综合以上分析可知,带电粒子第一次在磁场中运动时间范围是:
≤t′≤,其中:α=arctan,β=arctan;
答:(1)带电粒子第一次进入磁场的速度方向均与初速度方向成53°角.
(2)匀强电场的电场强度的大小为,方向平行于OM向左;
(3)若带电粒子射入电场的初速度vx≥v0 ,带电粒子第一次在磁场中运动的时间范围是≤t′≤(其中:α=arctan,β=arctan).



